3869. Meteomeasurements

Alex is studying in the fifth grade and is going to be a meteorologist. Alex recently started a diary, where he wrote the daily temperature in his own town. Alex found the historical data for the past several hundred years, which means that he has a lot of data. Alex asks you to write a program that calculates the average temperature during k consecutive days, and he needs these values for the entire observation period:

· Average temperature from 1-st till k-th day

· Average temperature from 2-nd till (k + 1)-th day

· and so on until he has data.

And after all these calculated values Alex needs only two numbers - the minimum and maximum values. Help Alex and write the program for him.

Input. First line contains two integers n and k – the number of temperature measurements and the number of days to calculate the average temperature (1 ≤ k ≤ n ≤ 10⁵). Next line contains n integers – the temperature measurements. Each of these numbers is in the range (-100, 100).

Output. Print two lines that contains minimum and maximum average temperature, calculated on segments of size k. Round the answer to the nearest integer.

Sample input	Sample output
4 2 10 12 18 16	11 17

SOLUTION

dynamic programming

Algorithm analysis

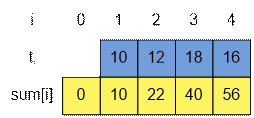
Let t₁, t₂, …, t_n be the observed temperatures. Calculate the partial sums of temperatures in array sum. That is let sum[i] = t₁ + t₂ +… + t_i (1 ≤ i ≤ n). For this we use the recurrence: sum[0] = 0, sum[i] = sum[i – 1] + t_i.

The average temperature from (i – k + 1)-th till i-th day (the length of the interval is k days) equals to (t_{i – k + 1} +… + t_i) / k = (sum[i] – sum[i – k]) / k. However, for simplicity, we will look for the minimum and maximum sums of temperature among all the intervals of length k (when we’ll print the average temperature, we’ll divide these values by k). That is, we compute:

· min =

· max =

So the minimum and maximum average temperature on intervals of length k equals to min / k and max / k.

Algorithm realization

Declare array of partial sums sum and infinity constant INF.

#define MAX 100010

#define INF 2000000000

int sum[MAX];

Read the input data.

scanf("%d %d",&n,&k);

Calculate the partial sums of temperature measurements.

sum[0] = 0;

for(i = 1; i <= n; i++)

{

scanf("%d",&val);

sum[i] = sum[i - 1] + val;

}

Calculate the minimum and maximum value among all the sums with k summands.

min = INF; max = -INF;

for(i = k; i <= n; i++)

{

if (sum[i] - sum[i - k] < min) min = sum[i] - sum[i - k];

if (sum[i] - sum[i - k] > max) max = sum[i] - sum[i - k];

}

Print the answer.

printf("%.0lf\n%.0lf\n",1.0*min/k,1.0*max/k);